要保证,这个矩阵乘这个矩阵的转置等于单位阵。
设M为元素取自交换体K中的n阶方阵,将M对角化,就是确定一个对角矩阵D及一个可逆方阵P,使M=PDP-1。设f为典范对应于M的Kn的自同态,将M对角化,就是确定Kn的一个基,使在该基中对应f的矩阵是对角矩阵。
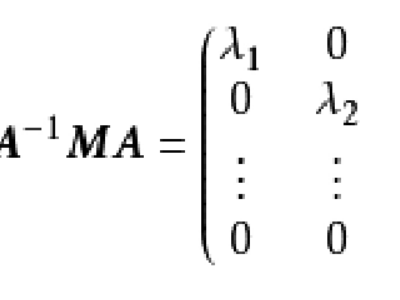
线性代数:
线性代数是数学的一个分支,它的研究对象是向量,向量空间(或称线性空间),线性变换和有限维的线性方程组。
向量空间是现代数学的一个重要课题;因而,线性代数被广泛地应用于抽象代数和泛函分析中;通过解析几何,线性代数得以被具体表示。
线性代数的理论已被泛化为算子理论。由于科学研究中的非线性模型通常可以被近似为线性模型,使得线性代数被广泛地应用于自然科学和社会科学中。
