1、具体定义自己看书,我们直接上手题目:
设对称矩阵
|4 2 2 |
A=|2 4 2 |
|2 2 4 |
求一个正交矩阵B,使B^TAB为对角矩阵,并写出该矩阵。
我们遇到这题目应该想到先求A的特征根,如下图所示
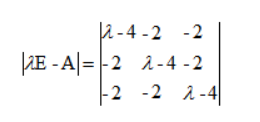

2、这里常用的矩阵求法为
1)这种3x3的矩阵可以按纵(横)列利用代数余子式展开直接求解,即


3、2)通过化为上三角或下三角(对于该题并不适用,过程太过繁琐)


4、由前面我们求得特征根的值为2和8(两个值重叠了,即2,2,8)
所以我们可得下图


5、现在我们对每个特征根带入原式求基础解系
具体来说就是原来的式子|入E-A|中的入应该被我们解出来的2,2,8重新带入
1)把入=2带入可得(2E-A)X = 0
即如下图所示

6、现在,我们就应该开始解这个其次方程了,由于不是我们的重点,而且小编以前写过关于其次和非齐次方程的解法,小编就在这里简单说一下,具体请看下面的连接。
我们得到的式子为-2x1-2x2-2x3=0;
把x1当作未知数,x2,x3为参数可得
-x1 = x2 + x3;
(x2,x3)把他们的取值分别设为(1,0)(0,1)可得x1的值为-1;
所以基础解系为X1(-1,1,0),X2(-1,0,1)
7、将X1,X2正交标准化得到:
正交标准话,即单位化(把括号里的每个数值除于图2)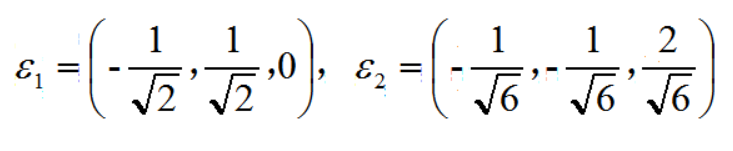
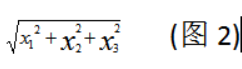
8、同理得到 入=8 的基础解系(自己动手解决看看哦),光看不算等于不看
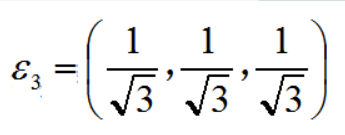
9、用解得的单位解组成正交矩阵
(注意:应该是纵向组成矩阵如图3)


