1、绘制曲线:
f[x_] :={5 Cos[x], 4 Sin[x]}
ParametricPlot[{f[x]}, {x, 0, 2 Pi}]

2、其实,每个点的切向量,都可以表示为:
g=D[f[x],x]
下面看一个互动效果:
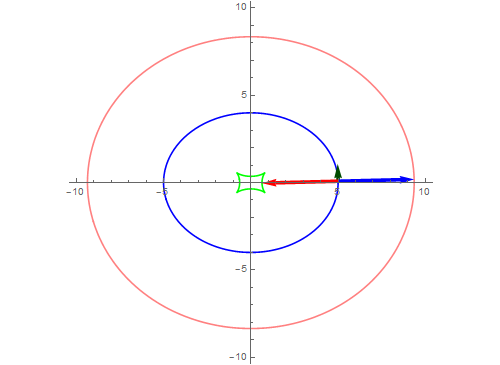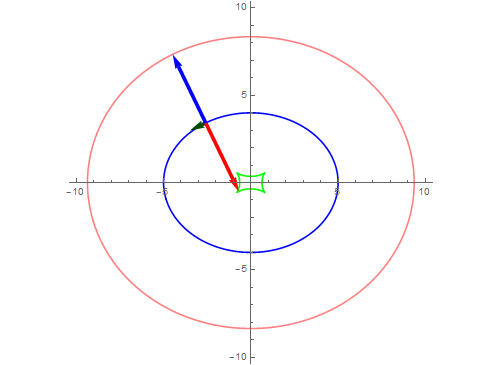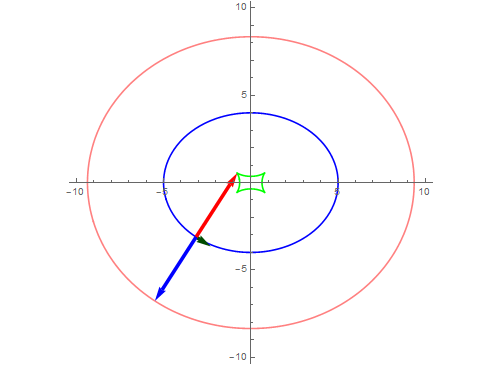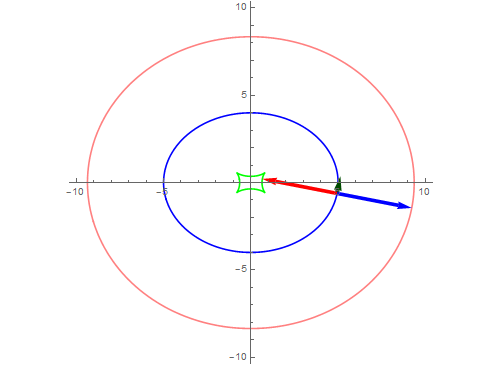
Manipulate[Show[
ParametricPlot[{f[x]}, {x, 0, 2 Pi}],
Graphics[{Arrow[{f[t], f[t] + g /. x -> t}]}]],
{t, 0, 2 Pi}]

3、规范切向量的长度:
Manipulate[
Show[ParametricPlot[{f[x]}, {x, 0, 2 Pi}],
Graphics[{Arrow[{f[t],
f[t] + Normalize@D[f[x], x] /. x -> t}]}]], {t, 0, 2 Pi}]

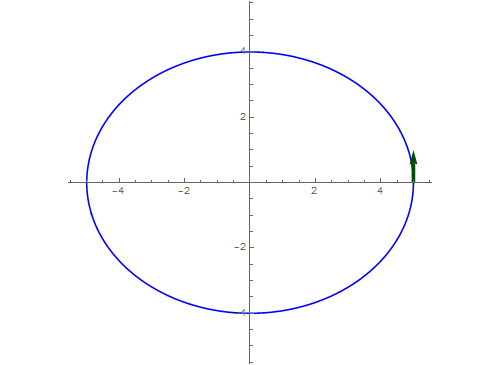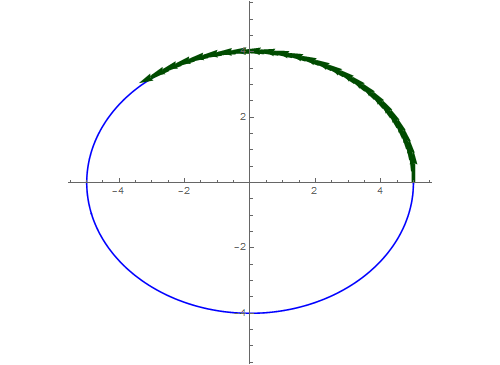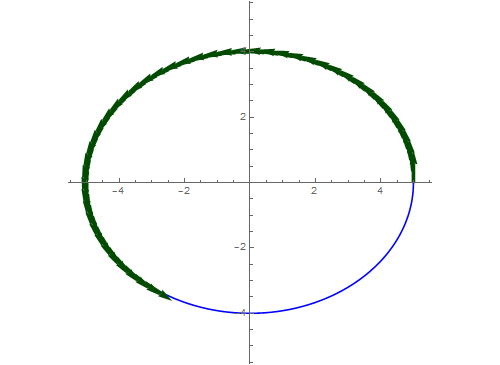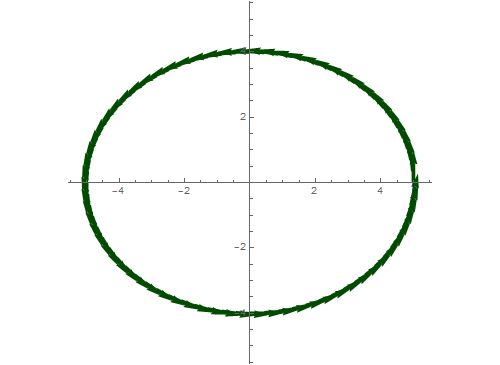
4、看一个动态图。
Manipulate[
Show[ParametricPlot[{f[x]}, {x, 0, 2 Pi}],
Graphics[{ Table[Arrow[{f[t],
f[t] + Normalize@g/. x -> t}], {t, 0, u,Pi/10}]}]],
{u, 0.02, 2 Pi, 2 Pi/100}]
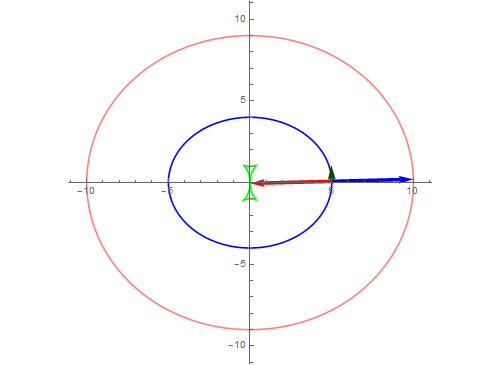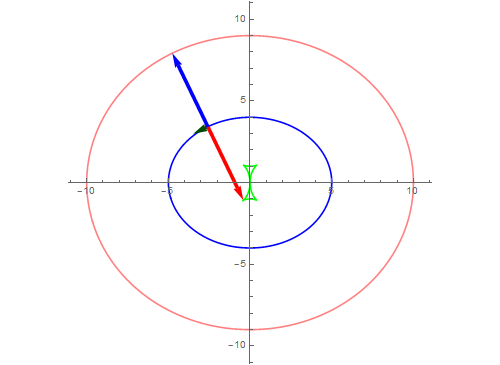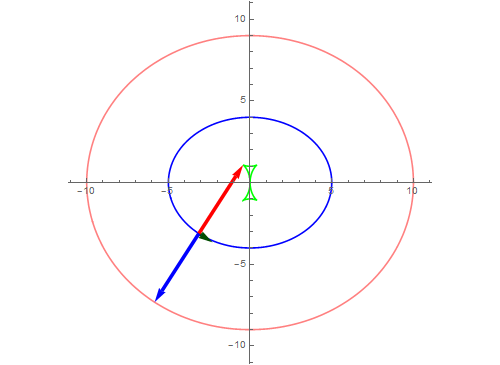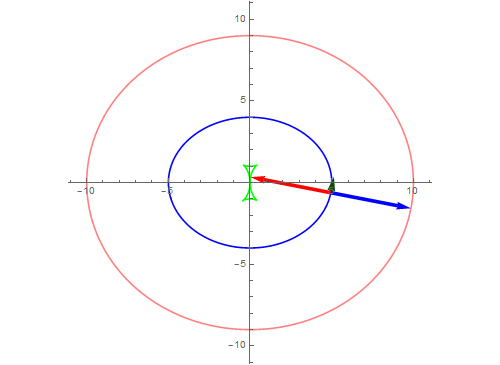
5、对单位切向量求导,就是曲线的法向量:
h[x_]:= FullSimplify[Normalize@g, Refine[Element[x, Reals]]]
把单位切向量和单位法向量都画出来:
Manipulate[
Show[ParametricPlot[{f[x]}, {x, 0, 2 Pi}],
Graphics[{Arrow[{f[t], f[t] + Normalize@g /. x -> t}],
Arrow[{f[t], f[t] - Normalize@D[h[x], x] /. x -> t}]}],
{t, 0.02, 2 Pi}]

6、等距曲线:
到已知曲线上的最短距离为定值的曲线。
g = FullSimplify[Normalize@D[f[u], u], Refine[Element[u, Reals]]];
Manipulate[
Show[ParametricPlot[{f[x], f[x] - Normalize@D[g, u] /. u -> x}, {x, 0, 2 Pi}],
Graphics[{
Arrow[{f[t], f[t] + Normalize@D[f[x], x] /. x -> t}],
Arrow[{f[t], f[t] - Normalize@D[g ,u] /. u -> t}]}]],
{t, 0.02, 2 Pi}]

7、等距曲线,当等距为3的时候,有下图做演示。
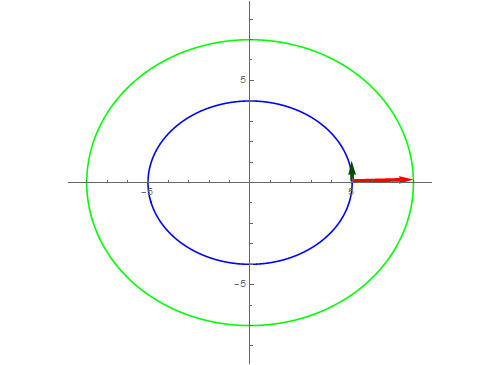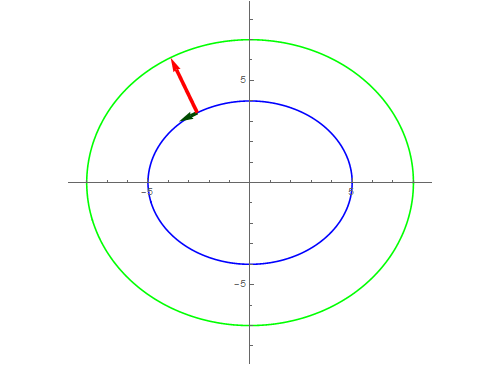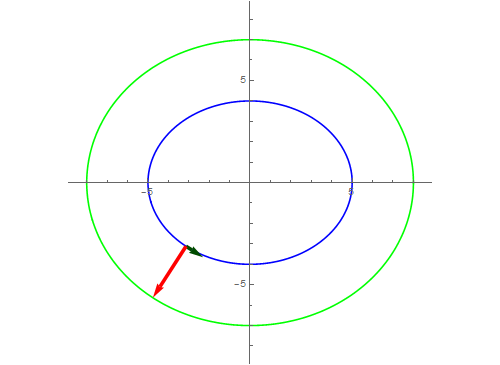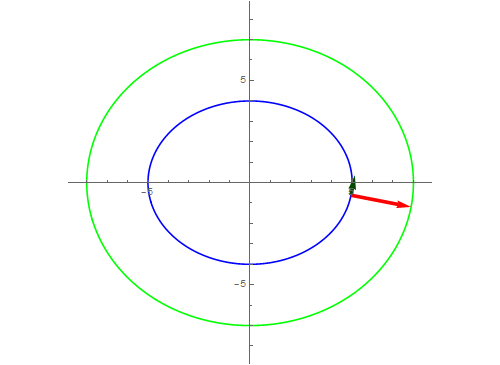
8、如果法向量指向反方向呢?
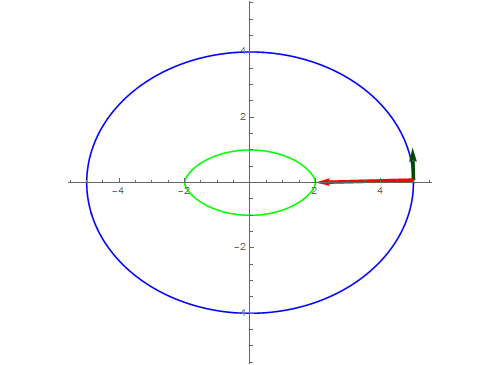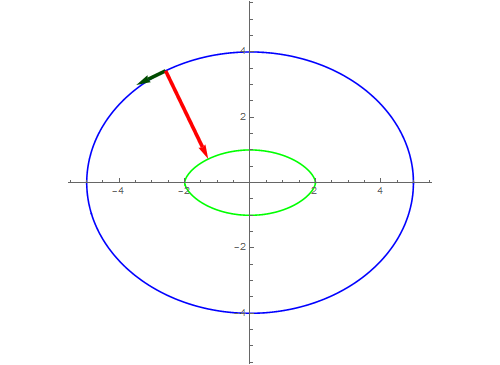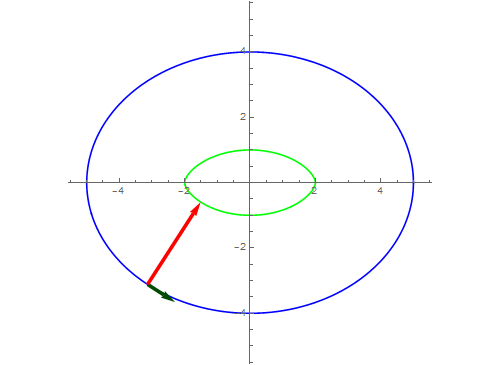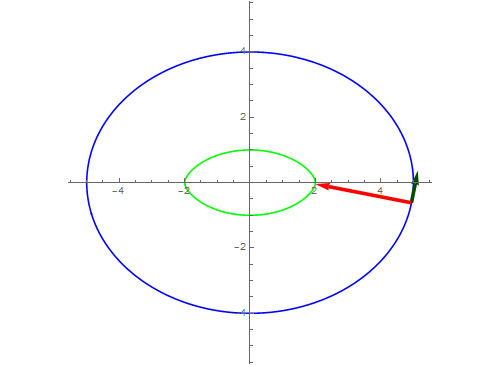
9、当等距大于4的时候,就只有一条等距曲线了。
下面分别是等距为5和4.36的情形。