1、我们用根号2、根号3、根号5来扩展有理数域Q为K。
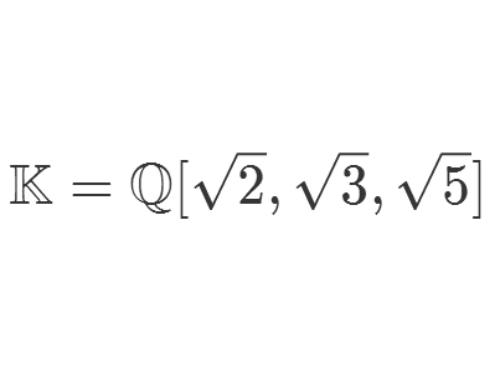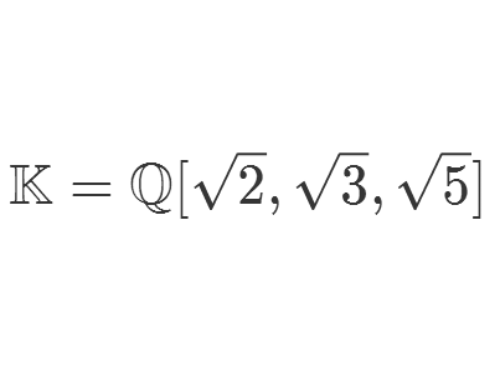
2、我们试图找到一个元素γ,可以独自把Q扩展为K。

3、根号2在有理数域的本原既约多项式记为f(x)。
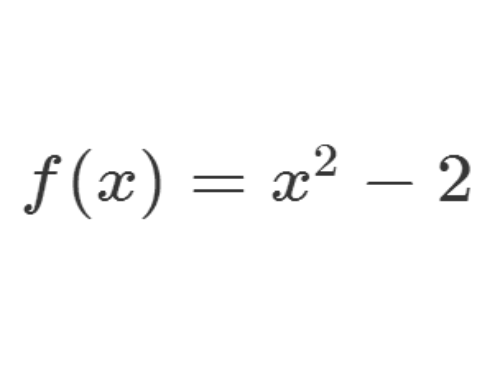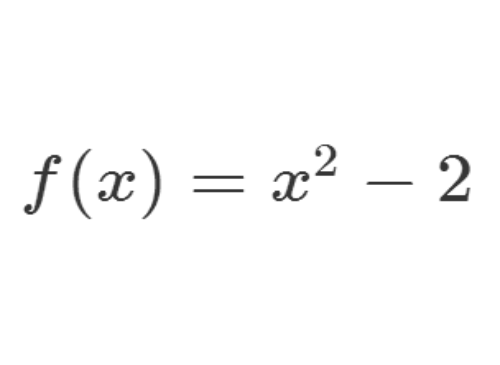
4、根号3的本原既约多项式记为g(x)。
5、我们根据g(x)来构造一个以根号2为根的多项式h(x)。

6、f和h只有一个根相同,那就是根号2,另一个根是不同的。

7、在域Q[sqrt(2)+sqrt(3)]里面分解多项式h(x)。这说明,根号2属于兑恶铼融Q[sqrt(2)+sqrt(3)]。同样的,根号3也属于Q[sqrt(2)+sqrt(3)]。所以,sqrt(2)+sqrt(3)是Q[sqrt(2),sqrt(3)]的一个本原元。

8、于是,要寻找K的本原元,只需要寻找Q[sqrt(2)+sqrt(3),sqrt(5)]的本原元。把sqrt(2)+sqrt(3)在有理数域的本原既约多项式记为p(x),把sqrt(5)在有理数域的本原既约多项式记为q(x),那么根据q(x)构造一个以sqrt(2)+sqrt(3)为根的多项式r(x)。r(x)和p(x)只有一个相同的根,且r(x)是Q[sqrt(2)+sqrt(3)+sqrt(5)]里面的可约多项式,可以分解因式。这说明,sqrt(2)+sqrt(3)属于Q[sqrt(2)+sqrt(3)+sqrt(5)],同样的,sqrt(5)也属于Q[sqrt(2)+sqrt(3)+sqrt(5)]。

9、综上所述,可以说明,sqrt(2)+sqrt(3)+sqrt(5)是K的一个本原元。当然,这个域还有很多其它本原元,这里不再一一列举。

