实数集包含所有有理数和无理数的集合就是实数集,通常用大写字母R表示。
18世纪,微积分学在实数的基础上发展起来。但当时的实数集并没有精确的定义。直到1871年,德国数学家康托尔第一次提出了实数的严格定义。任何一个非空有上界的集合(包含于R)必有上确界。
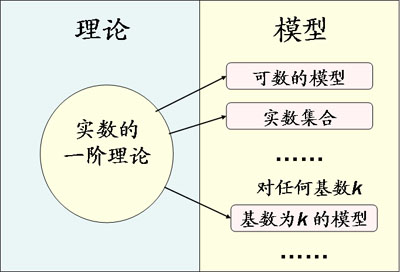
扩展资料:
1,加法定理:
1.1.对于任意属于集合R的元素a、b,可以定义它们的加法a+b,且a+b属于R;
1.2.加法有恒元0,且a+0=0+a=a(从而存在相反数);
1.3.加法有交换律,a+b=b+a;
1.4.加法有结合律,(a+b)+c=a+(b+c)。
2,乘法定理:
2.1对于任意属于集合R的元素a、b,可以定义它们的乘法a·b,且a·b属于R;
2.2乘法有恒元1,且a·1=1·a=a(从而除0外存在倒数);
2.3乘法有交换律,a·b=b·a;
2.4乘法有结合律,(a·b)·c=a·(b·c);
2.5乘法对加法有分配率,即a·(b+c)=(b+c)·a=a·b+a·c。
