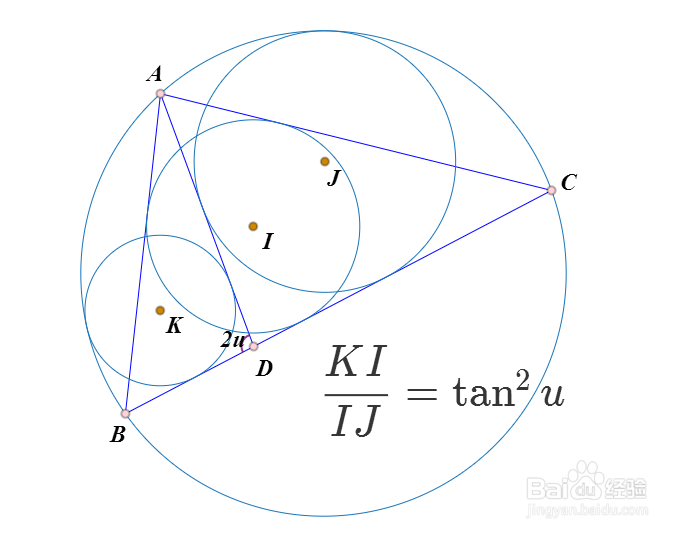
1、先介绍一下Thebault定理:
如下图,I、J、K三点共线,且KI:IJ=(tanu)^2。
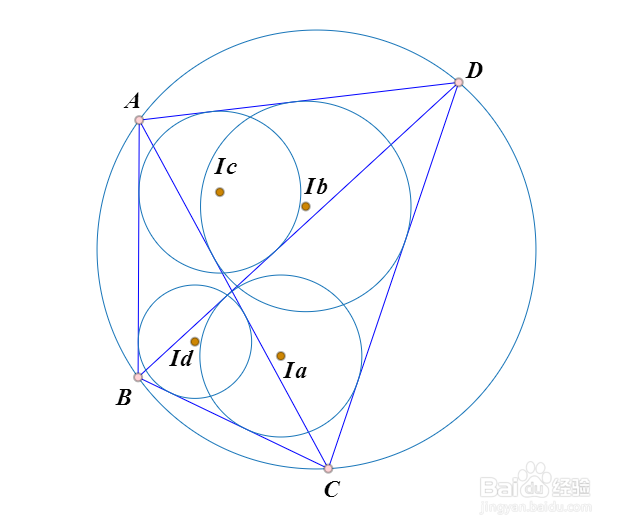
2、下面开始处理原题。
先标记题目中四个三角形内切圆的圆心是Ia、Ib、Ic、Id。
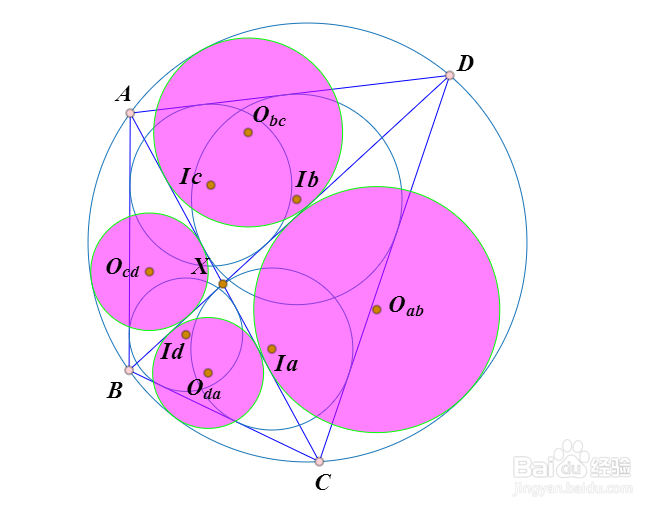
3、假设对角线AC和BD交于X。
与线段AX、BX及外接圆相切的圆的圆心记为Ocd,
类似的,有Oda、Oab、Obc。
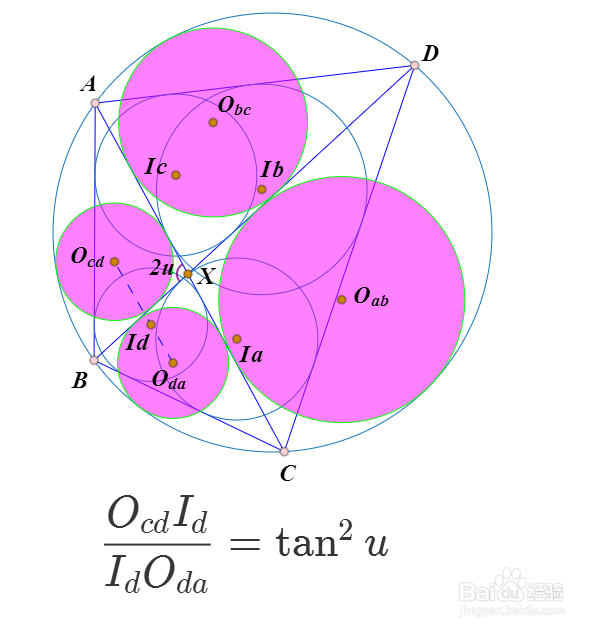
4、设AX与BX的夹角是2u,根据Thebault定理,可以证明:
Oda、Id、Ocd三点共线,且OcdId:IdOda=(tanu)^2。
5、同样的,Oab、Ia、Oda三点共线,且OabIa:IaOda=(tanu)^2。
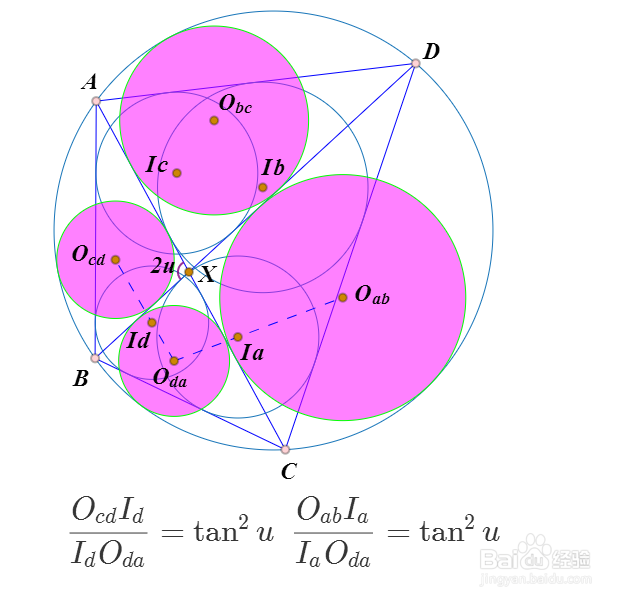
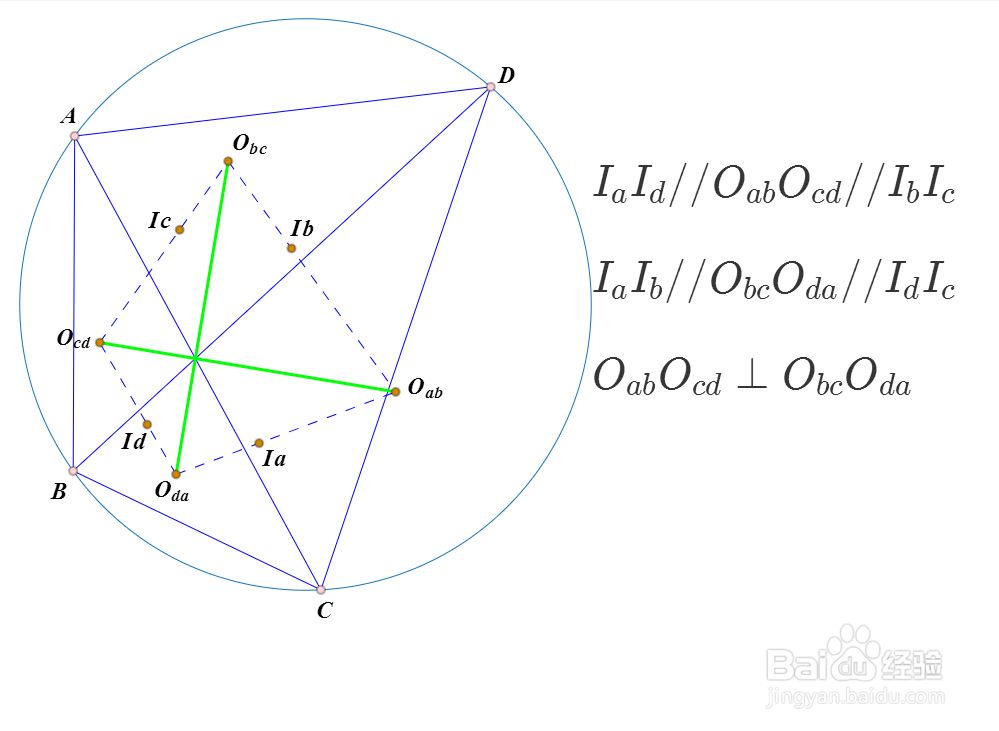
6、所以,IaId//OabOcd。

7、原题结论成立。