∵齐次方程y''-6y'+9y=0的特征方程是λ²-6λ+9=(λ-3)²=0
∴λ1=λ2=3
∵非齐次方程中3是特征方程的重根
∴特解y*=x²(ax²+bx+c)e^3x
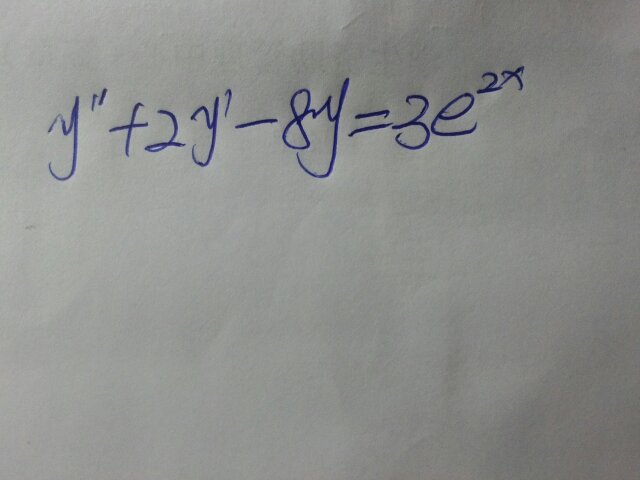
特点:
常微分方程的概念、解法、和其它理论很多,比如,方程和方程组的种类及解法、解的存在性和唯一性、奇解、定性理论等等。下面就方程解的有关几点简述一下,以了解常微分方程的特点。
求通解在历史上曾作为微分方程的主要目标,一旦求出通解的表达式,就容易从中得到问题所需要的特解。也可以由通解的表达式,了解对某些参数的依赖情况,便于参数取值适宜,使它对应的解具有所需要的性能,还有助于进行关于解的其他研究。
