1、输入数据：为了判断在都含有x1、x2、x3的两个正态总体之间，均值与方差是否具有显著的差异性，可以利用spss19.0导入数据并进行相应的分析以定性定量地分析两个总体间不同的指标的差异性。其中，在数据中增加一个变量t，在总体1中，t=1，而在总体2中，t=2，将，x1、x2、x3、t的数据导入到spss的数据编辑器中。
4、均值方差检验：然后使用分析—比较均值—独立样本T检验，打开对话框，选择x1、x2、x3为检验变量，t为分组变量，并且定义组1为1，组2为2，运行即可得到以下结果。
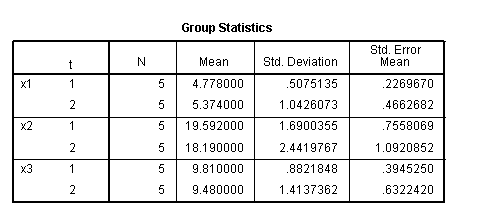
5、结果分析： 从独立性检验表格，可以看出，无论是假设方差相等还是方差不相等，x1、x2、x3的均值方程的t检验统计量对应的P值都不小，大于0.05，因此不能拒绝x1、x2、x3在总体1与总体2中相等的假设，认为x1、x2、x3在总体1与总体2中没有显著性差异。同样的，独立性检验表格也给出了方差检验的结果。x1、x2、x3的F统计量都比较小，可以通过检验，认为x1、x2、x3的方差在两个总体中都是是没有显著性差异的。
