1、其中n是实数。
如果n等于1,递归的初始点是{5,0},那么这个递归过程会快速进入稳定状态。
pts = NestList[F, {5, 0}, 20]

2、采用浮点数,是为了加速计算,但是误差就有可能失控,尤其出现混沌现象时。
不过,n等于1的时候,不会出现混沌。
作图:
ListLinePlot[NestList[F, {5, 0}, 100], PlotStyle -> Blue, PlotRange -> All]

3、如果递归的初始点是{3,0},那么,稳定位置仍旧是同一个地方。

4、具体算一下:
NestList[F, {3, 0}, 20]

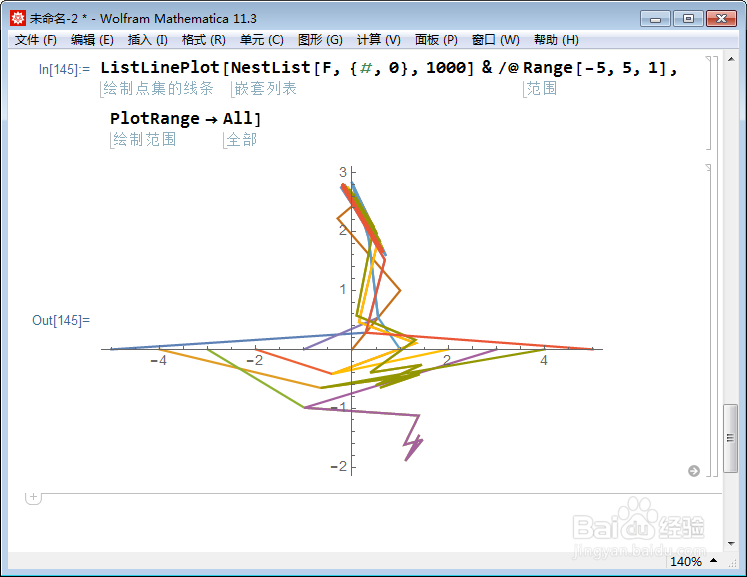
5、n等于2的时候,图像如下:

6、递归的初始点是{5,0}:
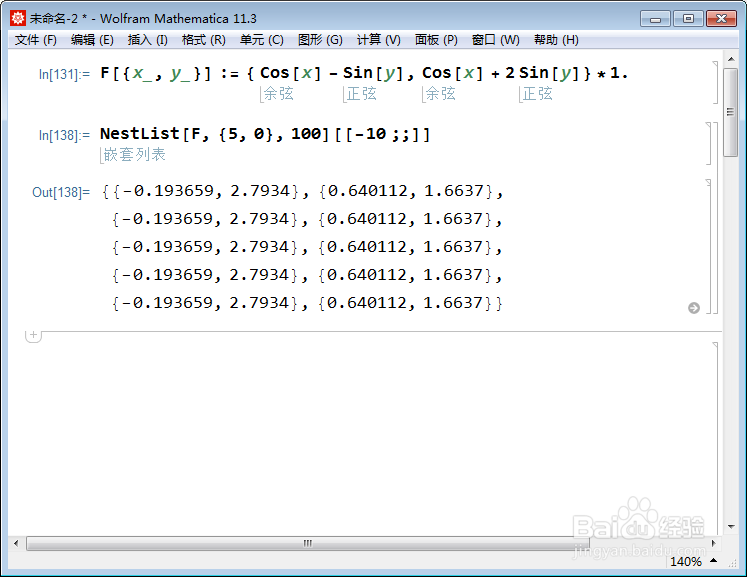
NestList[F, {5, 0}, 100][[-10 ;;]]
递归过程将进入两种状态的循环:
{-0.193659, 2.7934}, {0.640112, 1.6637}
7、不同的初始点,可能会遇到不同的循环状态。