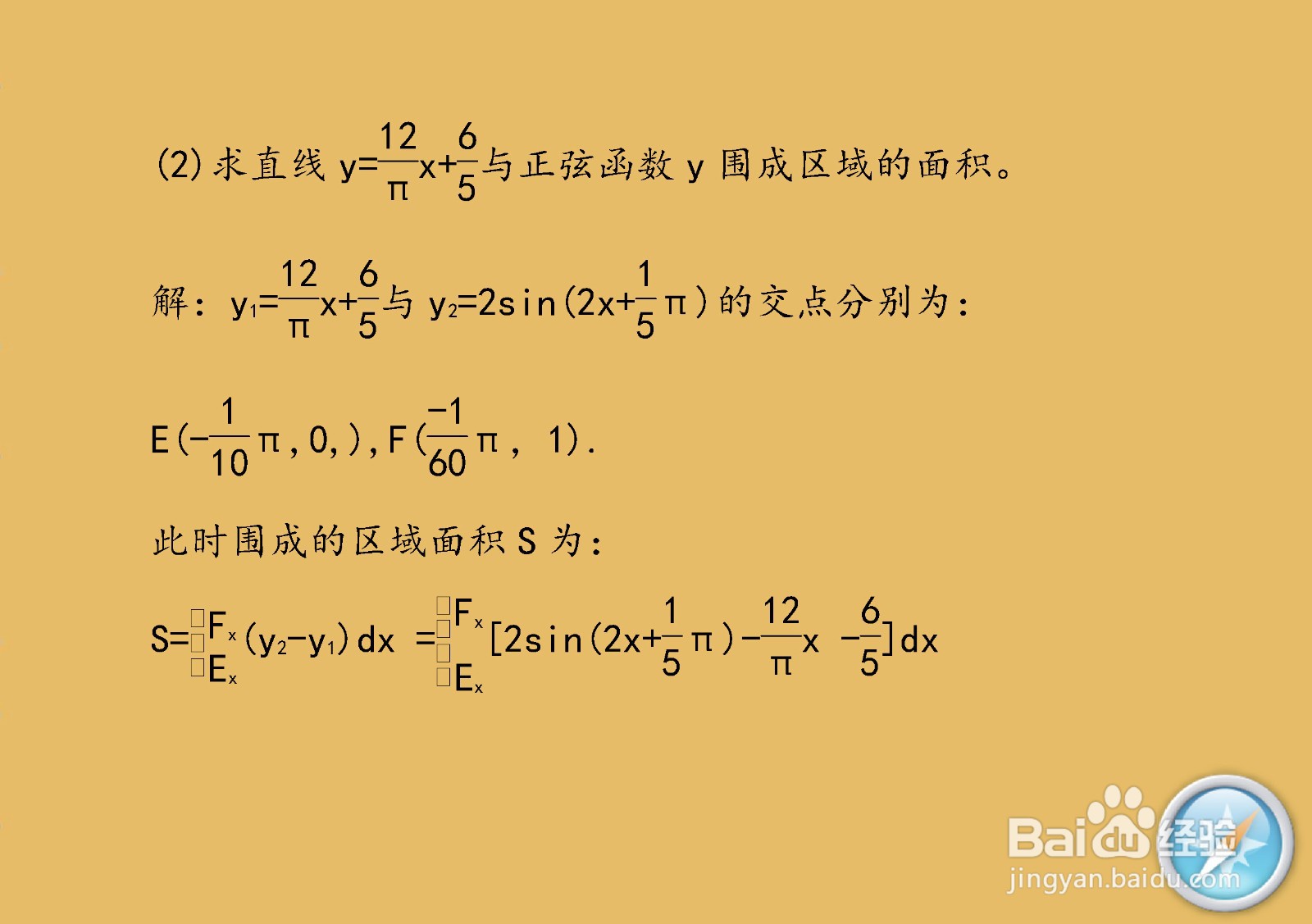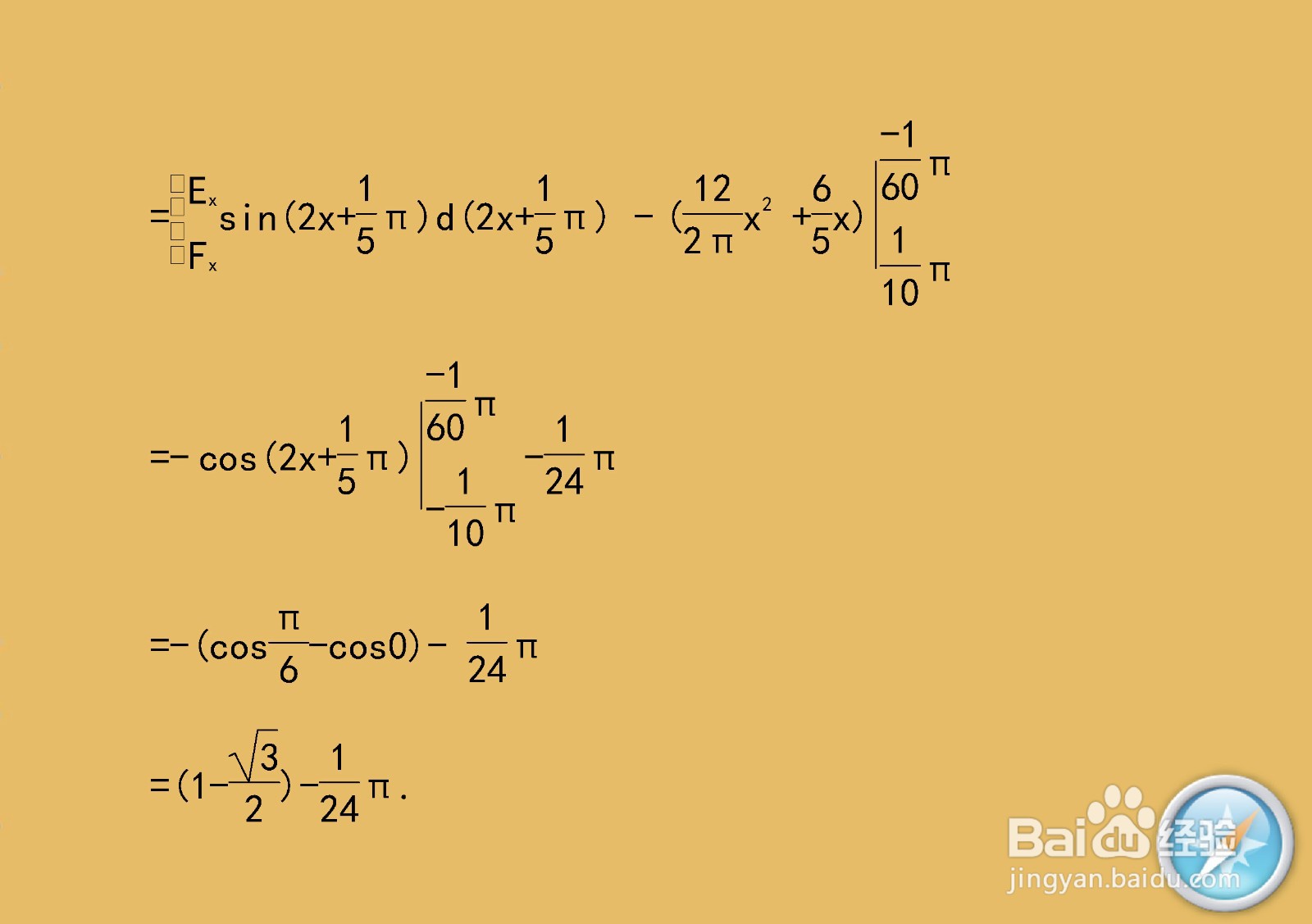1、 正弦三角函数的定义域、值域和最小正周期等基本性质如下。

2、正弦三角函数的对称轴和对称中心的求解。


3、由正弦函数的导数公式y=sinx,y'=cosx,即可求解该正弦函数的一阶导数、二阶导数,并和推解其高阶导数。

4、以基本正弦函数y=sinx的单调增区间和减区间,即可推导求出正弦复合函数的单调增区间和减区间。


5、用导数知识,求解函数在点A(-π/60,1)处切线的主要过程和步骤。

6、 根据导数的几何意义,求解函数在点B(21π/40,-√2)处切线的主要过程和步骤.
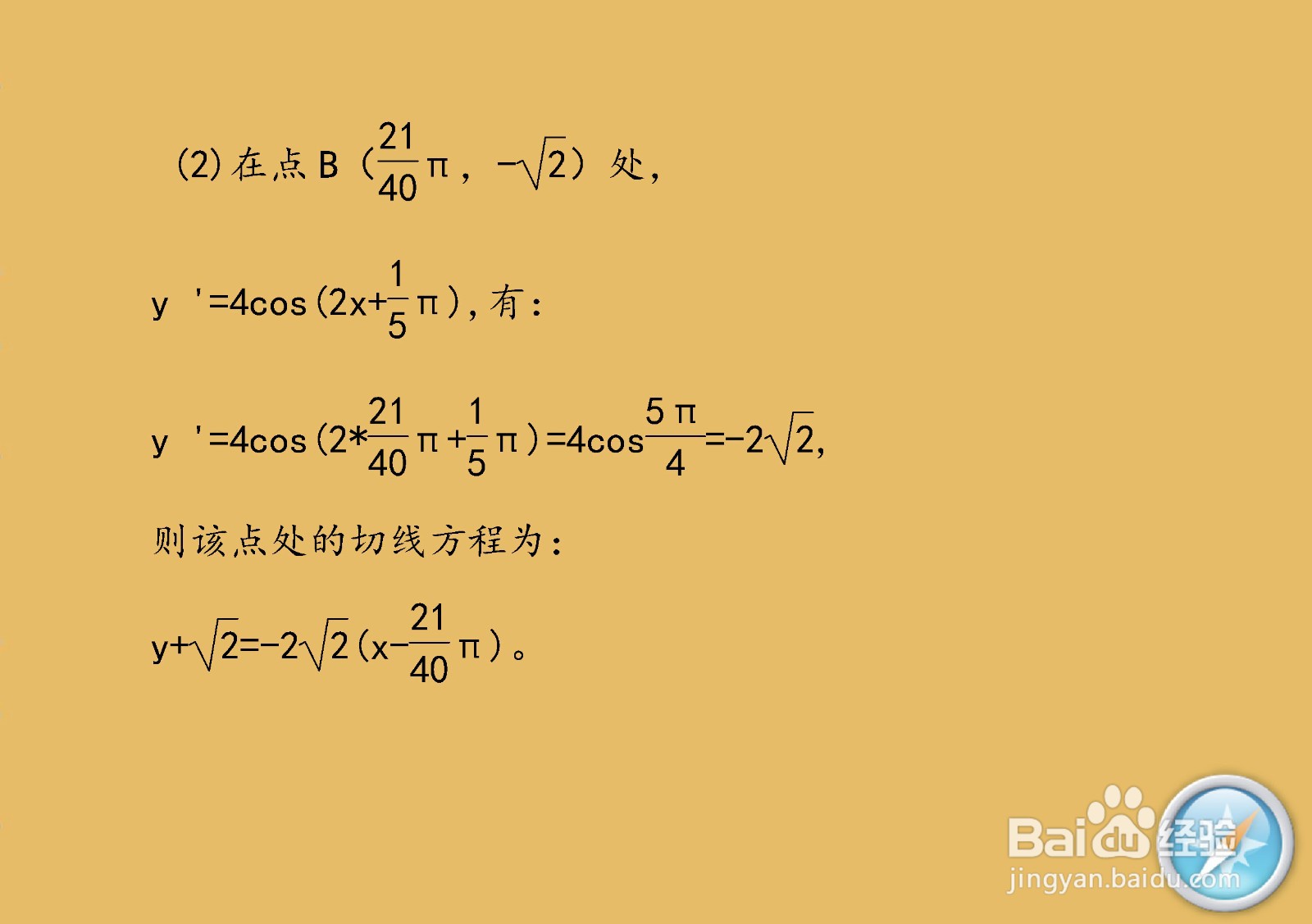
7、根据定积分有关知识,计算该正弦函数在半个周期的与坐标轴围成的区域的面积,主要过程如下:

8、继续使用定积分求面积知识点,举例介绍计算直线与正弦函数围成的区域面积的主要步骤。