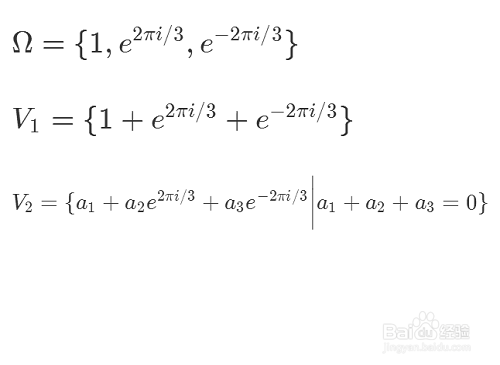1、声明这些向量空间是形式上的,是因为空间里面的向量之间的作用方式不明确,但是在群元素的作用下,集合的元素可以相互置换。在唁昼囫缍这些形式的向量空间里面,我们就不考虑向量的乘积等概念,只考虑群作用的结果和标量乘法。子空间V1是一个群不变的子空间。因为群作用下,Ω只是元素发生置换,元素不增不减,因而元素形式和保持不变,这说明群作用下V1的元素仍旧属于V1。
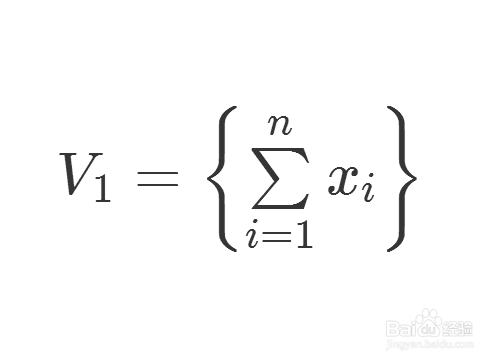
2、同样的理由,可以证明,V2也是群不变子空间。

3、要证明V是V1和V2的直和,就是证明V中的每一个向量v可以用一个V1里面的向量v1和V2里面的向量v2表示出来。这无非就是在域K里面解一个方程组。
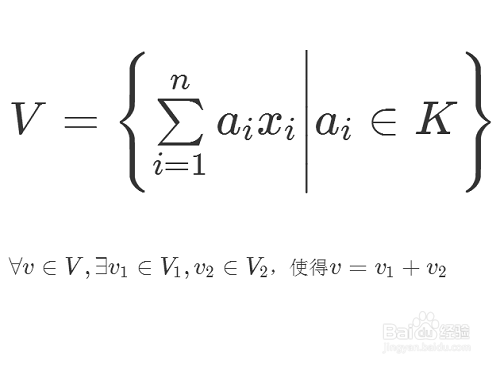
4、假设G在V、V1、V2里面的表示分别记为φ、φ1、φ2。那么φ就是后二者的直和。
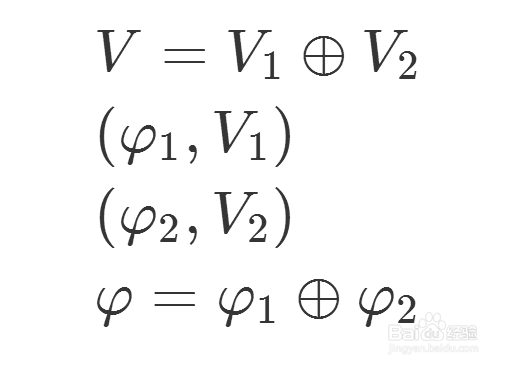
5、如果把两种表示对应的矩阵表示记为Φ、Φ1、Φ2,那么Φ就可以记为Φ1和Φ2的直和。
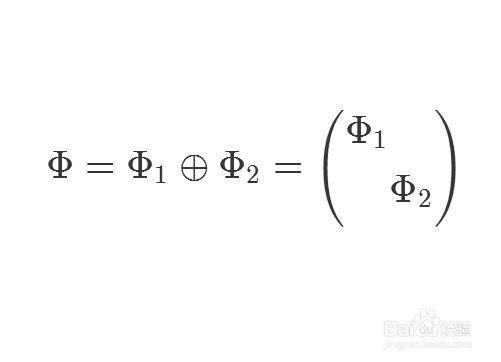
6、如果给定Ω的元素是复平面上某个正三角形的三个顶点,那么,V1和V2就可以表示为如下形式,原则上可以据此给出对称群S3的一个2次表示。