1、我们要寻找本原元素,主要就是为了证明八阶域的乘法群是循环群。
下面,我们将把每一个非零元素,用b的幂表示出来,以此说明b是一个本原元素。
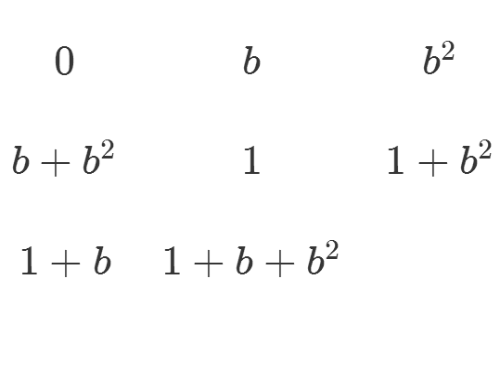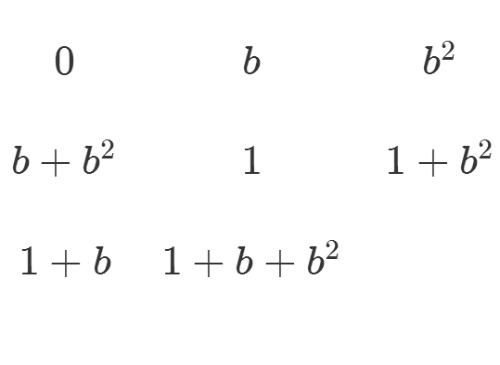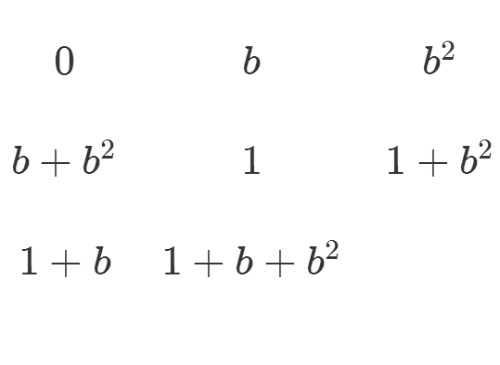
2、在八阶域里面,仍旧沿用二阶域的一个特性,1+1=0。
在八阶域里面,1+b可以写为b的三次方。

3、在八阶域里面,1+b+b^2可以写为b的5次方。

4、在八阶域里面,b+b^2可以写为b的4次方。

5、在八阶域里面,1+b^2可以写为b的6次方。
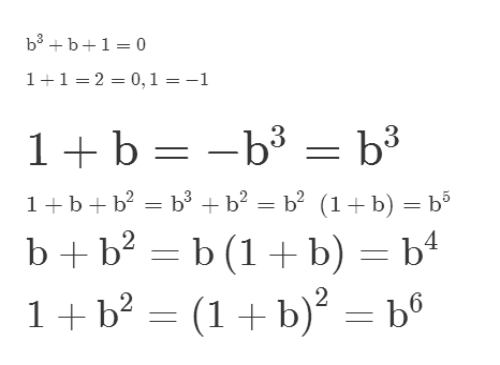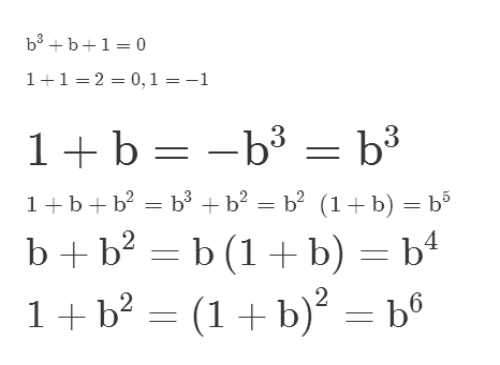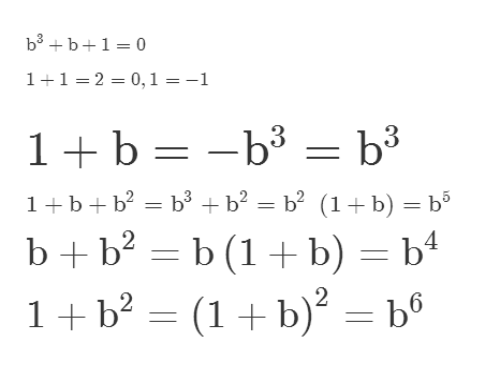
6、于是,可以重写八阶域。
其中,在八阶域里面,b^7=1,因此b是七阶元素。
本来呢,七阶循环群的每一个不等于1的元素都是生成元。但是如果b是实根的话,b的正整数次方经过mod2的运算,是不可能出现虚数的。因此,实根不可能是本原元素。

7、八阶域里面,每一个非实数的元素,都是本原元素,一共有四个本原元素。
