1、先计算y关于x的一阶导数:
y'=dy/dx=(dy/dt)/(dx/dt)

2、用Mathematica套公式:
yx=D[y,t]/D[x,t]
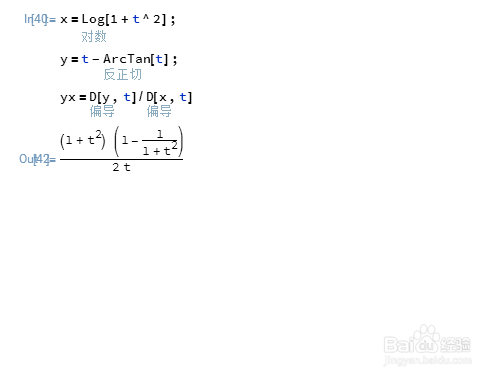
3、化简一下:
yx=D[y,t]/D[x,t]//FullSimplify
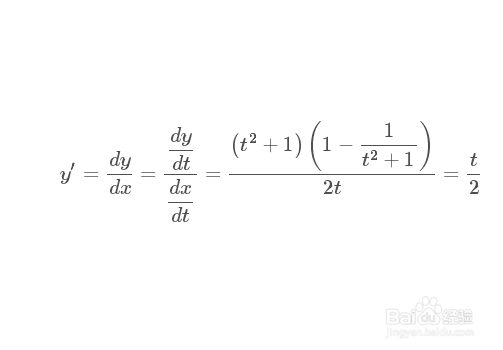
4、二阶导数,其实就是求y的一阶导数关于x的导数:
y''=dy'/dx=(dy'/dt)/(dx/dt)

5、在Mathematica里面套公式:
yxx=D[yx,t]/D[x,t]
这样,我们就得到答案了。

6、而上面的过程,在Mathematica里面,可以整合:
x=Log[1+t^2];y=t-ArcTan[t];yxx=D[D[y,t]/D[x,t],t]/D[x,t]//FullSimplify

