1、 最简单的情形是Euler定理:三角形外接圆半径R,内切圆半径r,外心、内心距离d,等价于d^2=R^2-2Rr。
当大圆、小圆的半径和圆心距满足“心距公式”——d^2=R^2-2Rr——的时候,那么,有无数个三角形既内接于大圆,又外切于小圆(如图A);
“心距公式”得不到满足的时候,没有三角形既内接于大圆,又外切于小圆。事实上,线段EF的包络线是大圆、小圆所确定的共轴圆系里面的一个圆(如图B、C)。
大家能不能作出EF与其包络线的切点?
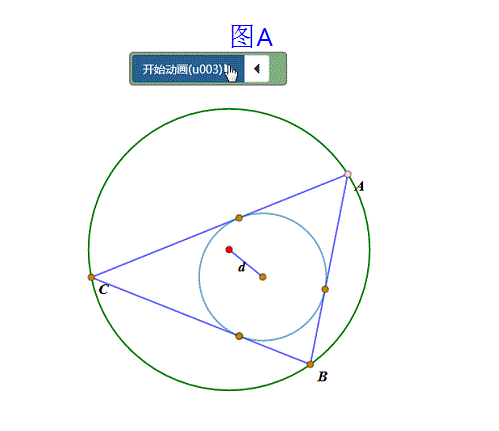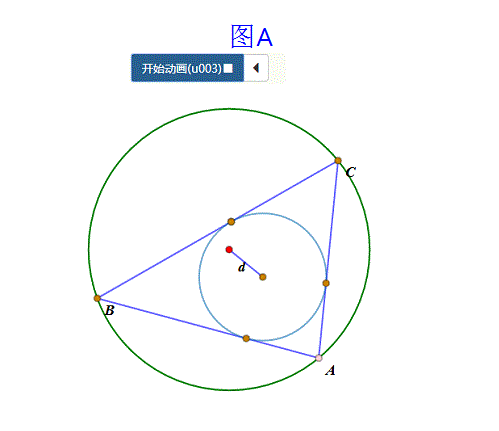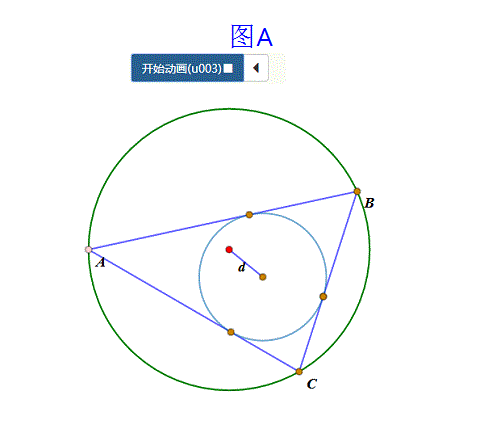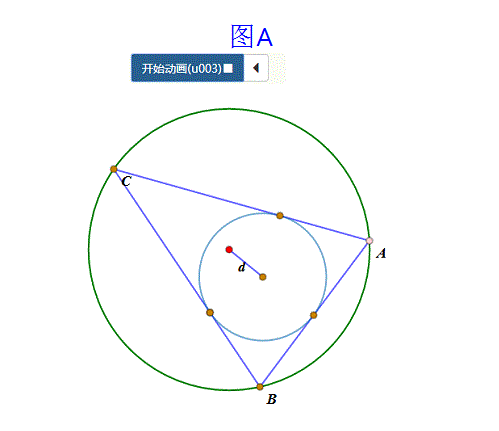


2、 三角形与椭圆的情形:
我的方法比较投机,先作椭圆,再作椭圆的内接三角形及其内接圆,然后经过仿射变换,使内切圆变成椭圆!
网络画板的保存过程可视化了!



3、 三角形与双曲线的情形,由于双曲线的图形是无界的,所以课件不太稳定。


4、 “双心四边形”情形:
具体步骤见《双心四边形的作图、性质》,这里只考虑“心距公式”——1/(R+d)^2+1/(R-d)^2=1/r^2。
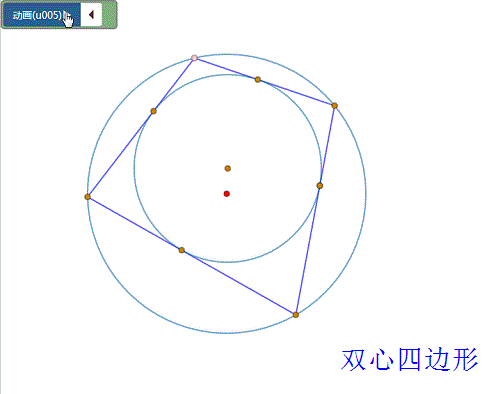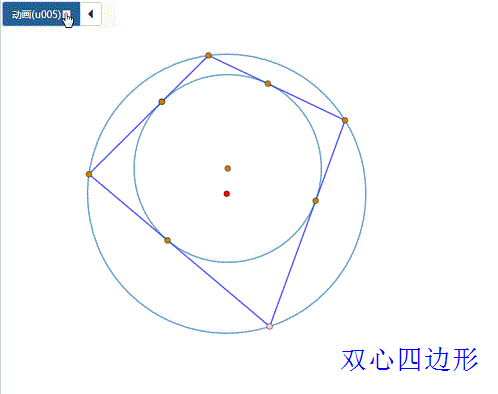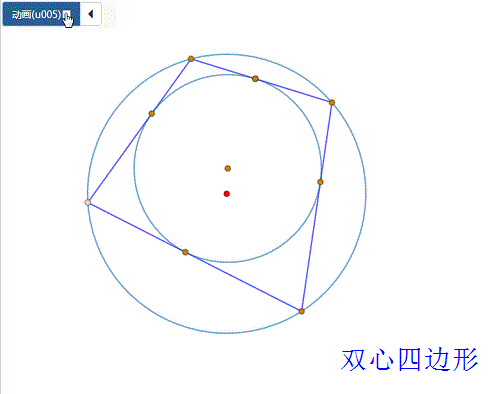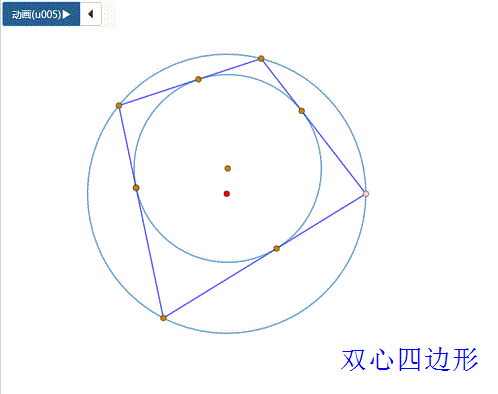



5、 椭圆与四边形情形:
由于目前网络画板不能构造轨迹椭圆的切线(难办了),所以只好继续用“仿射变换”了。


