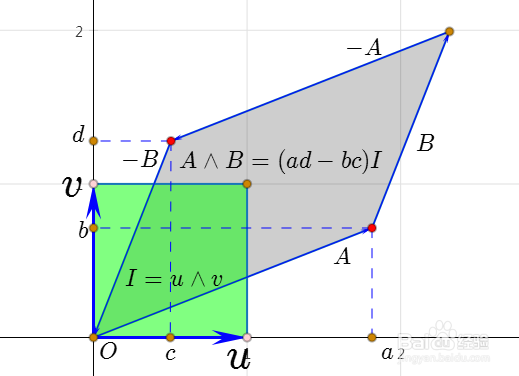
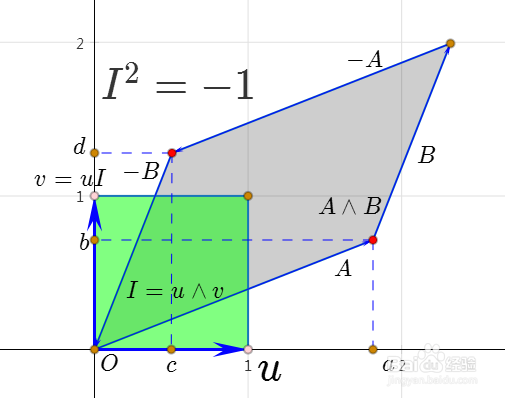
1、A和B的外积,记为A⋀B,它的几何意义是由向量A和B围成的有向平行四边形。
我们称之为双向量。
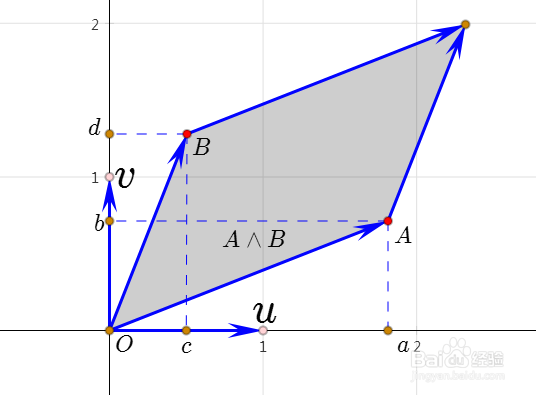
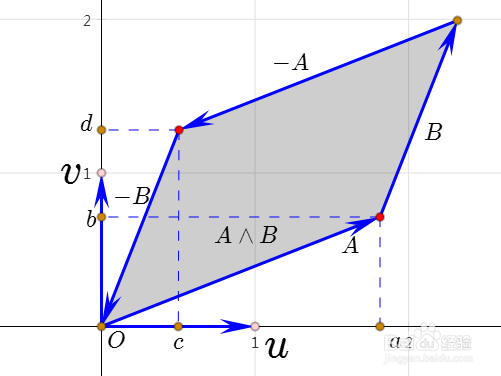
2、根据定义,再结合图像,可以证明:
A⋀B=B⋀(-A)=(-A)⋀(-B)=(-B)⋀A
注意它们代表同一个有向平行四边形即可。
3、u⋀v称为二维空间的单位双向量,代表面积为1的有向平行四边形。

4、一般的,我们把n维向量空间里的r个线性无关向量的外积称为r-向量,
把n-向量称为这个空间的伪标量。
特别的,我们把二维空间里的双向量称为其伪标量。
单位伪标量的平方等于-1。
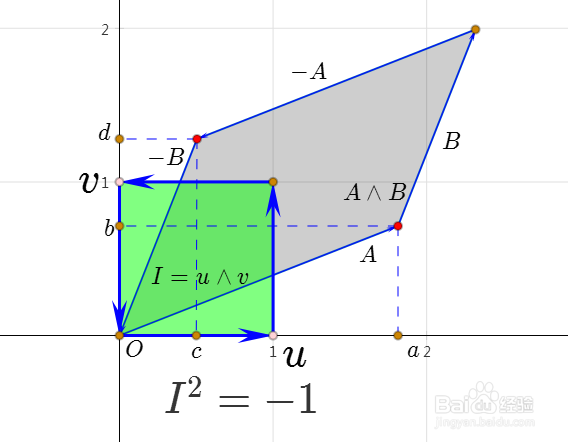
5、I^2=-1,所以,可以说I带有虚数单位的一些性质。
比如,uI相当于把向量u绕原点逆时针旋转90°。
6、这样,单位伪标量就有了两个几何意义:
1、有向的平行四边形;
2、旋转90°的算子。
如果I代表第一个意义,那么A⋀B相对于I的大小,就具体的代表有向面积。
A⋀B=(ad-bc)I